Analiza portfelowa. Bezpieczne inwestycje. Gra na giełdzie

Krzywa portfeli efektywnych

Marek Wierzbicki

Gra na Giełdzie, listopad 1996

Ze wszystkich inwestycji możliwych do skonstruowania z wielu walorów, tylko niektóre są akceptowane przez racjonalnych inwestorów. Zysk i obarczone nim ryzyko muszą zapewniać realizację preferencji różnych inwestorów. Każdy z nich oczekuje przy tym, że ponosząc pewne ryzyko osiąga najwyższy możliwy do osiągnięcia zysk. Takie połączenie oczekiwań możliwe jest tylko na krzywej portfeli efektywnych. Wielu inwestorów ciekawi jednak, co się dzieje na całej krzywej. Jak zmieniłby się skład portfela w przypadku podniesienia bądź obniżenia akceptowanego ryzyka. Interesujące jest również, czy sąsiedni portfel na krzywej zawiera te same akcje czy też zupełnie różne.

W poprzednim odcinku tego cyklu opisywałem znaczenie poszczególnych portfeli teoretycznych. Przypomnę, że różnią się one od siebie nie tylko poziomem zysku i ryzyka ale również i nachyleniem krzywej, które determinuje stosunek relatywnych zmian ryzyka i zysku. Przejście od portfela o niższym ryzyko do portfela o wyższym ryzyku oznacza zwiększanie agresywności inwestycji. W dzisiejszym artykule zajmę się podobnym samym problemem - wyjaśnię co się dzieje z portfelem, gdy przesuwamy się po krzywej portfeli efektywnych w górę lub w dół. Przedstawię jednak inne spojrzenie na sprawę. Tym razem zwrócę uwagę na zmiany składu portfeli, a nie na zmiany jego parametrów takich jak zysk, ryzyko czy pochodna. Na zakończenie pokażę jak można oszacować przybliżony przebieg krzywej portfeli efektywnych znając tylko portfele minimalnego ryzyka i rynkowy.

Przejścia fazowe w modelu Markowitza

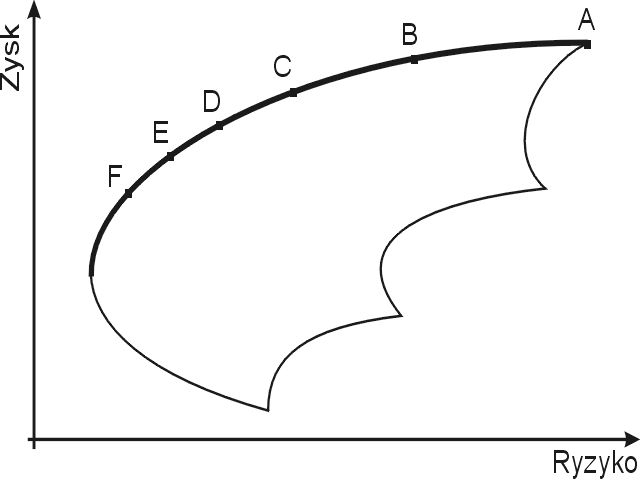
Prezentowałem już w tym cyklu artykułów przykładowy wygląd mapy ryzyko-zysk. Dzisiaj przedstawiam taką mapę ponownie, zwaracam jednak uwagę na inne szczegóły. Górna, pogrubiona krawędź mapy to krzywa portfeli efektywnych. W poprzednim artykule zwracałem uwagę na teoretyczne znaczenie portfeli na tej krzywej. Dziś zwrócę uwagi na składy portfeli na poszczególnych odcinkach krzywej. Na rysunku 1, na krzywej portfeli efektywnych zaznaczone są punkty przejść fazowych (A..F):

Aby w pełni wyjaśnić pojęcie przejść fazowych opiszę zmiany składu portfeli w miarę zmian jego położenia na krzywej portfeli efektywnych. Rozpocznijmy analizę od środka odcinka krzywej CD. Powiększony fragment rysunku 1, wraz z większą liczbą szczegółów przedstawiony jest na rysunku 2:

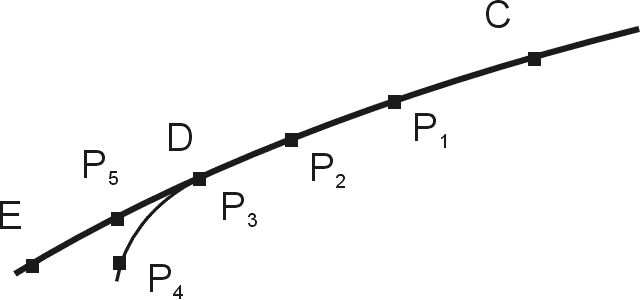
Załóżmy, że wstępnie wybraliśmy portfel P₁ leżący na tym odcinku, jako dopuszczalny dla naszych preferencji inwestycyjnych. W skład tego portfela wchodzą akcje R, S, T i U w proporcjach: 15% R, 25% S, 40% T i 20% U. Obawiamy się jednak, że wybrany portfel obarczony jest zbyt wysokim ryzykiem i rozważamy przesunięcie się w dół krzywej, w celu obniżenia ryzyka. Po zmianie położenia portfela na krzywej (portfel P₂) okazało się, że jego skład jest następujący: 15% R, 30% S 40% T i 15% U. Po dalszym obniżeniu położenia na krzywej portfel (P₃) doszedł do punktu D i miał w nim skład: 15% R, 35% S, 40% T i 10%U. Załóżmu, że ryzyko tego portfela dalej nie satysfakcjonuje nas i pragniemy obniżyć je jeszcze bardziej. Jakiekolwiek manipulowanie składem, z udziałem tylko akcji R, S, T i U nie umożliwia nam jednak obniżenia ryzyka z jednoczesnym pozostaniem na krzywej efektywnej. Co prawda portfel P₄ o składzie 15% R, 40% S, 40% T i 5% U ma ryzyko mniejsze niż ryzyko poprzedniego portfela P₃, nie leży on jednak na krzywej portfeli efektywnych. Oznacza to, że można skonstruować portfel (w tym wypadku P₅) o tym samym ryzyku, który będzie posiadał jednocześnie wyższą stopę zwrotu. Widać przy tym, że droga którą poszlibyśmy zmieniając wyłącznie skład ilościowy portfela (proporcje procentowe między akcjami) przy stałym składzie jakościowym (tylko akcje określonego wcześniej rodzaju, czyli w naszym przypadku R, S, T i U) "odkleja się" od krzywej efektywnej i przechodzi w głąb obszaru możliwych portfeli, czyli w rejony zdominowane przez inne portfele. Wróćmy więc do punktu D i portfela P₃, który się w nim znajduje. Jak należałoby zmienić skład portfela P₃, aby przesunąć się dalej po krzywej portfeli efektywnych do portfela P₅. Okazuje się, że będzie to możliwe dopiero po dodaniu nowej, nie uwzględnianej wcześniej spółki. Portfel P₅ ma skład: 10% R, 40% S, 40% T, 5% U i 5% W. Aby pozostać na krzywej efektywnej musieliśmy więc zastosować zmianę jakościową składu portfela - dodać nową firmę. Punkt w którym dokonywana jest zmiana składu jakościowego nazywa się punktem przejścia fazowego na krzywej portfeli efektywnych. Na naszej przykładowej mapie ryzyko-zysk przedstawionej na rysunku 1 punkty przejść fazowych oznaczone są literami od A do F. Jak można się domyśleć z mojego wywodu wszystkie odcinki między przejściami fazowymi mają stałe składy jakościowe, oczywiście różne na poszczególnych częściach. Cały czas należy przy tym pamiętać, że opisywane odcinki krzywej o stałym składzie jakościowym z łączącymi je przejściami fazowymi w żaden sposób nie są powiązane z podziałami teoretycznymi - portfel rynkowy czy krytyczny może wypaść zarówno w środku odcinka jak i na przejściu fazowym.

Z opisywanym problemem związane są jeszcze dwie sprawy praktyczne. Pierwsza to zmiana składu portfela w punkcie fazowym. We wcześniejszej części artykułu opisywałem znaczenie przejścia fazowego na przykładzie dodawania nowej akcji do już egzystujących w portfelu. Możliwa jest też sytuacja odwrotna, kiedy to odejmuje się akcję. Występuje ona wtedy, gdy udział akcji spada do zera a krótka sprzedaż nie jest możliwa - akcja przestaje być uwzględniana. Ponadto warto zwrócić uwagę na punkt A na przykładowej mapie z rysunku 1. Punkt ten określa położenie portfela składającego się z jednej akcji, o najwyższej możliwej stopie zwrotu. Jest on jednocześnie punktem fazowym krzywej portfeli efektywnych - w tym miejscu od razu zostaje dodana druga firma.

Pozostało tylko zastanowić się, jak wiele punktów fazowych może znaleźć się na krzywej efektywnej. Dla polskiej giełdy w chwili obecnej, jeśli weźmie się pod uwagę wszystkie firmy otrzymujemy od 30 do 40 przejść fazowych (w zależności od horyzontu czasowego). Jeśli uwzględnimy tylko akcje rynku równoległego otrzymujemy od 5 do 15 punktów. Największe znaczenie ma tu liczba uwzględnianych walorów - w miarę jej wzrostu maleje względna liczba przejść fazowych (stosunek liczby przejść do liczby wszystkich akcji).

Przybliżenie krzywej portfeli efektywnych

W kilku poprzednich odcinkach tego cyklu zwracałem uwagę na fakt, że model Sharpe'a jest pewnym uproszczeniem modelu Markowitza, skonstruowanym w celu przyspieszenia analizy przy maksymalnie niewielkim zafałszowaniu rzeczywistości. Dążąc do dalszego przyspieszenia i uproszczenia Grinold i Kahn zaproponowali sposób tworzenia krzywej efektywnej bazujący wyłącznie na składzie portfeli minimalnego ryzyka i rynkowego. Mimo tego, iż odnoszą oni swoje uproszczenie do modelu indeksowego, można je zastosować w każdym modelu egzystującym w przestrzeni ryzyko-zysk.

Podstawą uproszczenia Grinolda i Kahna jest założenie (bazujące na założeniach modelu CAPM), że na krzywej portfeli efektywnych są tylko dwa punkty przejść fazowych - w portfelu minimalnego ryzyka i w portfelu rynkowym. Wszystkie portfele znajdujące się pomiędzy tymi punktami są kombinacją liniową portfeli krańcowych i mają stały skład jakościowy. Udowadniają przy tym, że ryzyko dowolnego portfela z krzywej efektywnej może być wyznaczone z użyciem wzoru 1:

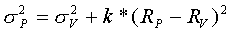
gdzie:

• ryzyko poszukiwanego portfela (odchylenie standardowe)
• ryzyko portfela minimalnego ryzyka
• współczynnik nadmiaru ryzyka
• zadana stopa zwrotu portfela
• stopa zwrotu portfela minimalnego ryzyka

  W równaniu 1 stała k jest współczynnikiem określającym nadmiar ryzyka w poszukiwanym portfelu w stosunku do portfela minimalnego ryzyka. Wyznacza się ją ze wzoru 2: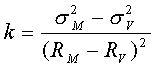

  

  gdzie:

  • współczynnik nadmiaru ryzyka
  • ryzyko portfela rynkowego (odchylenie standardowe)
  • ryzyko portfela minimalnego ryzyka
  • stopa zwrotu portfela rynkowego
  • stopa zwrotu portfela minimalnego ryzyka

  Praktyków interesuje zapewne, jak ma się przybliżona krzywa portfeli efektywnych do rzeczywistej krzywej. Rozbieżności przedstawiam na rysunku 3:

  

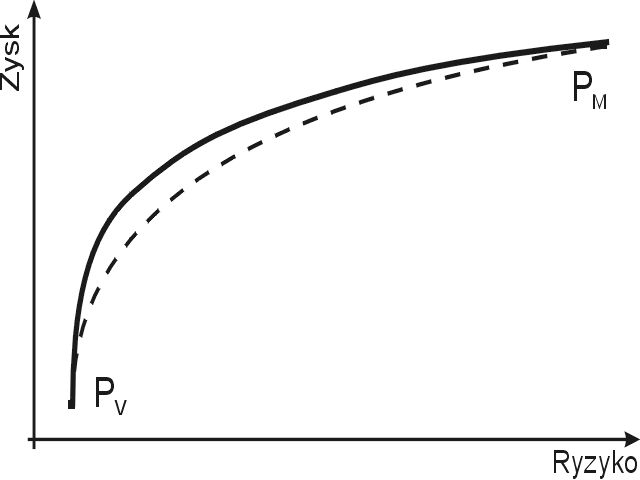
  Krzywa kropkowana reprezentuje przybliżenie krzywej efektywnej znajdującej się powyżej. Jak należało się spodziewać, przybliżenie krzywej jest bliskie faktycznym portfelom efektywnym w okolicach portfeli minimalnego ryzyka P_V i rynkowego P_M. Największe rozbieżności występują w środku analizowanego odcinka. Mimo to różnice między ryzykiem rzeczywistego portfela efektywnego w środku krzywej a jego przybliżeniem nie są większe niż kilka procent wartości rzeczywistej.

  Skład portfeli przybliżonych

  Ostatnią sprawą, na którą chciałbym zwrócić uwagę, to praktyczny sposób wyznaczania składu portfeli z przybliżonej krzywej efektywnej. Grinold i Kahn zaproponowali również rozwiązanie i tego problemu. Znając składy portfeli krańcowych i stopę zwrotu poszukiwanego portfela można wyznaczyć udziały poszczególnych akcji w poszukiwanym portfelu ze wzoru 3:

  

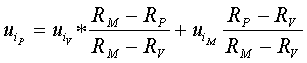
  gdzie:

  • udział akcji i w poszukiwanym portfelu
  • udział akcji i w portfelu minimalnego ryzyka
  • udział akcji i w portfelu rynkowym

  Oczywiste jest to, że w skład poszukiwanego portfela wejdą tylko akcje z obu krańcowych portfeli i nie ma sensu wyliczać udziałów dla innych spółek (będą one równe zero).

  Podsumowanie

  Po tych wszystkich rozważaniach przydałaby się czytelnikom odpowiedź czy te informacje są komukolwiek w ogóle potrzebne. Otóż tak. Zacznijmy od przejść fazowych. Ich wyznaczenie umożliwia lepsze kształtowanie własnych inwestycji. Dobrym przykładem jest tu sytuacja, gdy konstruujemy portfele optymalne z uwzględnieniem wszystkich spółek notowanych na giełdzie i eliminujemy z dopuszczalnych inwestycji najgorsze fundamentalnie spółki. Chcielibyśmy przy tym, aby w naszym portfelu było jak najmniej tych niepożądanych firm. Co prawda, zawsze sugeruję odwrotną kolejność działania, to znaczy najpierw eliminacja złych firm, a dopiero później konstrukcja portfeli, jednak kolejność odwrotna też ma swoje zalety. Umożliwia na przykład zaakceptowanie składów o niewielkim udziale firm niepożądanych, bez których inwestycja znacząco pogorszyłaby swoje parametry.

  Inną sprawą jest przybliżenie krzywej efektywnej. Otóż uważam, że powinno się ją stosować wyłącznie w celu oszacowania ryzyka poszukiwanego portfela. Poleganie na składzie portfela, zwłaszcza w rejonach odległych od portfela rynkowego i minimalnego ryzyka może być dość zawodne. Oczywiście, w przypadku, gdy nic innego nie jest możliwe lepszy taki portfel, niż wybrany przypadkowo.