Analiza portfelowa. Bezpieczne inwestycje. Gra na giełdzie

Jednoindeksowy model Sharpe'a

Marek Wierzbicki

Gra na Giełdzie, maj 1996

W ciągu kilkanastu lat po opublikowaniu teorii Markowitza dotyczącej wyboru portfeli optymalnych trwały wśród teoretyków rozważania, czy zaproponowana przez niego model jest jedynym możliwym opisem rynku. Głównym nurtem prac było poszukiwanie takiej metody konstruowania portfeli, która dawałaby równie dobre efekty jak model Markowitza, przy prostszym i szybszym sposobie konstruowania portfeli. Rok 1963 przyniósł znaczący przełom w postaci jednoindeksowego modelu giełdy opracowanego przez Williama Sharpe'a. Zyskał on sobie dużą popularność dzięki swojej prostocie, nie wpływającej w znaczący sposób na jakość wyników.

Po pierwszej fascynacji teorią Markowitza pojawiły się problemy z praktycznym jej zastosowaniem. W przypadku analizowania portfeli o znanym składzie zawierających kilku walorów, wyznaczenie ich parametrów jest jeszcze dość prostą operacją. Kiedy jednak weźmiemy pod uwagę polską giełdę, na której notowane jest ponad 70 akcji okaże się, że zachowanie tych akcji opisane jest z wykorzystaniem ponad dwóch i pół tysiąca parametrów. Dla giełdy na której notowane jest 1000 akcji (a na Wall Street jest ich jeszcze więcej) ich zachowanie opisane jest za pomocą ponad 500 tysięcy parametrów. Nietrudno się domyślić, że taka liczba informacji może w czasie wyboru portfela optymalnego doprowadzić do bólu głowy nawet największy i najszybszy komputer. Teoretycy rozpoczęli więc poszukiwania modeli dających zadowalające rezultaty przy zmniejszeniu ilości informacji potrzebnej do praktycznego zastosowania.

Historycznie rzecz ujmując pierwsze propozycje uproszczenia swojego modelu do postaci indeksowej zaproponował sam Markowitz. Bez wchodzenia w szczegóły dopuszczał on aby zachowanie poszczególnych akcji traktować jako linię regresji odnoszoną do zmian pewnego (nieokreślonego) indeksu ogólnego według wzoru:

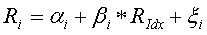(1)

Formalnie model został zaproponowany i opisany przez Sharpe'a a rozwinięty przez Johna Lintnera. Podstawy propozycji Sharpe'a wynikały z praktycznych doświadczeń, które wykazywały, że zachowanie poszczególnych akcji może być wytłumaczone z użyciem jednego syntetycznego czynnika opisującego zachowanie całej giełdy. Sharpe zauważył, że większość akcji zmienia swoją wartość zgodnie z zachowaniem całej giełdy. Jeśli więc cała giełda spada - większość akcji również spada. W przypadku wzrostu większość akcji rośnie. Przełomowym wydarzeniem było zwrócenie uwagi na fakt, że akcje które tracą na wartości szybciej niż indeks giełdowy (który opisuje w pewien sposób zachowanie całej giełdy) również zyskują na wartości szybciej niż ten indeks. Podobnie akcje spadające wolniej niż indeks rosną wolniej od niego. Od tego momentu było już bardzo blisko do wyznaczenia matematycznego opisu zachowania akcji w zależności od zmian indeksu giełdowego. Opis ten uzależnia stopę zwrotu od trzech składników: stałego - niezależnego od zmian na rynku; zmiennego - proporcjonalnego do zmian indeksu giełdowego, przy czym można wyznaczyć współczynnik proporcjonalności nazwany beta oraz składnika losowego o zmianach nie dających wytłumaczyć się z użyciem wykorzystywanych parametrów. Składnik stały wyjaśnia w praktyce długookresowy trend zmian cen poszczególnych akcji. Jeśli więc cena akcji wzrosła w okresie, w którym indeks giełdowy pozostawał w trendzie poziomym zachowanie to tłumaczone jest właśnie przez ten parametr (nazywany rezydualną stopą zwrotu i oznaczany alfa). Współczynnik proporcjonalności opisuje zmiany wartości akcji następujące zgodnie ze zmianami wartości indeksu giełdowego. Parametr beta opisuje przy tym siłę zależności zachodzących między zmianami indeksu, a opisywanym walorem. Jeśli beta wynosi 0.8 oznacza to, że zmianie indeksu o 1% odpowiada zmiana wartości akcji o 0.8% (przy założeniu, że alfa jest równa zero). Oczywiście zależność ta obowiązuje zarówno w przypadku wzrostu jak i spadku indeksu giełdowego. Ostatni składnik opisu (losowy) wprowadzony został w celu wyjaśnienia ruchów akcji niezgodnych z modelem. Równanie opisujące zachowanie akcji w zależności od zmian zachodzących na giełdzie powinno być skonstruowane w taki sposób, aby wpływ składnika losowego był jak najmniejszy. Sytuacja taka występuje przy dobrym dopasowaniu bety do rzeczywistości. Doprowadziło to do zaadaptowania znanego ze statystyki wzoru używanego w metodzie najmniejszych kwadratów, umożliwiającego wyznaczenie parametru beta akcji:

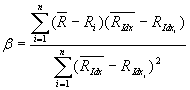(2)

gdzie:

• liczba analizowanych okresów (sesji), które służą do stworzenia opisu zachowania akcji.
• stopa zwrotu akcji w i-tym okresie
• stopa zwrotu indeksu w i-tym okresie
• średnia stopa zwrotu akcji
• średnia stopa zwrotu indeksu

Niektórzy autorzy sugerują również możliwość wyznaczania bety z użyciem całkowitego ryzyka akcji i indeksu, choć osobiście uważam ten pomysł za nie najlepszy:

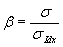(3)

gdzie:

• całkowite ryzyka akcji
• całkowite ryzyko indeksu

Znając betę można wyznaczyć alfę akcji:

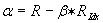(4)

Do pełnego obrazu sytuacji powinniśmy oszacować zachowanie składnika losowego każdej akcji. Przyjmuje się, że wartość oczekiwana składnika losowego jest równa zero (jeśli alfa wyznaczana jest z użyciem wzoru 4 jest to prawda). Oznacza to, że składnik ten nie wpływa na zyskowność akcji - oczywiście w ujęciu długookresowym. Można to tłumaczyć w ten sposób, że akcja czasami rośnie szybciej niż to wynika z opisu matematycznego, czasami wolniej, lecz po odpowiednio dużej liczbie obserwacji jej zachowanie zostanie uśrednione do zachowania modelowego. Możemy przy tym wyznaczyć odchylenie standardowe składnika losowego czyli ryzyko tego, że faktyczne zachowanie będzie się różniło od zachowania modelowego. Ryzyko to jest nazywane ryzykiem specyficznym akcji i może być wyznaczone ze wzoru (zastosowane oznaczenia są zgodne z wcześniejszymi):

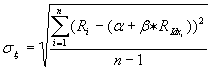(5)

Zamiast skomplikowanego wzoru wyznaczającego ryzyko specyficzne w sposób bezpośredni możemy skorzystać z równania uzależniającego ryzyko całkowite akcji od ryzyka rynkowego, bety i ryzyka specyficznego:

(6)

Ryzyko specyficzne wyznaczone ze wzorów (5) i (6) jest równoważne. Wzór (6) ma również zastosowanie do portfeli składających się z większej liczby akcji. Analiza wzoru (6) dla portfela nasuwa kilka wniosków. Jak widać na całkowite ryzyko portfela wpływa iloczyn ryzyka indeksu i bety (ryzyko rynkowe lub systematyczne) oraz ryzyko specyficzne (zwane dywersyfikowalnym). Nazwa pochodzi stąd, że obniżanie ryzyka całkowitego poprzez dodawanie kolejnych firm do portfela (przy zachowaniu stałej bety) wynka właśnie z obniżania ryzyka specyficznego.

W modelu Sharpe'a najważniejszym współczynnikiem jest beta, opisująca zachowanie waloru w zależności od zachowania całego rynku. W przypadku gdy spodziewamy się hossy należy inwestować w akcje posiadające wysokie współczynniki beta. Pozwoli to nam na przyrost naszych kapitałów szybszy od przyrostu giełdy. Jeśli obawiamy się bessy (jednak jej prawdopodobieństwo nie jest zbyt wysokie) powinniśmy inwestować w papiery o niskiej becie. W przypadku wzrostu na giełdzie da to nam niezbyt szybki wzrost naszych kapitałów zabezpieczy nas jednak w przypadku załamania notowań. Oczywiście kiedy spodziewamy się, że bessa nadejdzie na pewno, zamiast akcji powinniśmy inwestować w obligacje. W tabeli zaprezentowane są charakterystyczne wartości bety wraz z opisem zachowań walorów:

Zakres bety	Opis zachowania akcji z betą z tego zakresu
b<0	Akcja zachowuje się przeciwnie niż indeks który posłużył do jej wyznaczenia (czyli ogólnie rynek) to znaczy na ogólny wzrost giełdy akcja reaguje spadkiem wartości. Jak się można domyślić akcje o ujemnej becie muszą stanowić na rynku mniejszość, żeby nie zdominowały zachowania całej giełdy
b=0	Stopa zwrotu akcji jest statystycznie niezależna od rynku - oznacza to, że akcja jest pozbawiona ryzyka rynkowego. Oczywiście w praktyce nie oznacza to, że akcja nie zmienia swojej wartości, tylko że czasami zachowuje się zgodnie z zachowaniem giełdy a czasami przeciwnie. Taki parametr jest też charakterystyczny dla obligacji rządowych bądź lokat bankowych.
0<b<1	Walor defensywny - reaguje na zmiany giełdowe wolniej niż rynek.
b=1	Akcja podlega z punktu widzenia statystyki dokładnie takim samym zmianom jak cała giełda. W praktyce oznacza to, że czasami zmiany są gwałtowniejsze a czasami wolniejsze niż na rynku.
b>1	Akcja agresywna i ryzykowna. Wzrostowi giełdy towarzyszy szybszy wzrost wartości akcji. Jednocześnie jednak spadek na giełdzie jest wiązany z szybszym spadkiem tej akcji.

W swoich rozważaniach Sharpe przyjął, że każdy inwestor będzie się zachowywał rozważnie i będzie uwzględniał istnienie obligacji jako ewentualne ubezpieczenie przed stratami. Założył też przy tym, że stopa zwrotu akcji rekompensuje ryzyko ponoszone w czasie inwestowania na giełdzie. Biorąc pod uwagę sytuację idealną (to znaczy taką, że zachowanie akcji da się wytłumaczyć bez udziału składnika losowego) najniższe możliwe ryzyko pojedynczego waloru można wyznaczyć jako iloczyn ryzyka całej giełdy i parametru beta. W związku z tym, że ryzyko całej giełdy jest jednakowe dla wszystkich akcji łatwo się domyślić, że dla Sharpe'a miernikiem ryzyka stała się wartość współczynnika beta danej akcji. Tak więc akcje o wysokiej becie powinny charakteryzować się wyższą stopą zwrotu, aby były równie atrakcyjne jak walory bardziej stabilne. Jeśli uwzględni się istnienie alfy okaże się, że najlepsze (najefektywniejsze) będą akcje o wysokiej stopie zwrotu i niskiej becie.

Pora teraz przejść do tej części modelu, która wprowadza największe ułatwienia w analizie portfelowej. Jak zapewne czytelnicy pamiętają, do wyznaczenia ryzyka portfela trzeba było znać korelacje wszystkich par akcji wchodzących w jego skład. W modelu indeksowym możemy zastosować znany z modelu Markowitza wzór kowariancyjny, jeśli pamiętamy w jaki sposób powiązane są bety i kowariancje:

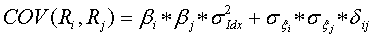(7)

We wzorze (7) poza znanymi parametrami, takimi jak beta, ryzyko całkowite indeksu i ryzyko specyficzne występuje korelacja szczątkowa między składnikami losowymi (w teorii zakłada się, że jej wartość jest równa zero, czyli składniki losowe są do siebie ortogonalne).

Oczywiście takie podejście nie dawałoby nam żadnych korzyści wynikających z zastosowania uproszczenia modelu. Do wyznaczenia ryzyka całkowitego portfela lepiej skorzystać ze wzoru (6) i z równania opisującego jego betę:

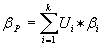(8)

gdzie:

• liczba akcji w portfelu
• udział akcji i w portfelu

Wyznaczenie ryzyka portfela jest więc w tym przypadku dużo łatwiejsze - wystarczy zsumować bety akcji wchodzących w skład portfela (z uwzględnieniem wag udziałów w tym portfelu) a następnie pomnożyć tą betę przez ryzyko indeksu giełdowego. Jeśli uważamy, że portfel nie jest idealnie zdywersyfikowany (posiada na przykład zbyt mało akcji) należy dodatkowo uwzględnić ryzyko specyficzne portfela:

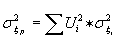(9)

Jak widać uproszczenie w procesie wyznaczania ryzyka jest znaczące. Do zachowania pełnego obrazu portfela należy pamiętać o jego rezydualnej stopie zwrotu (czyli alfie):

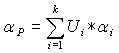(10)

Konstruując model zachowania akcji należy pamiętać, że duże znaczenie ma wybór indeksu, który posłuży za bazę do modelu indeksowego. Modelowe zachowanie akcji (dobór parametrów alfa i beta) realizowane jest w ten sposób, że ryzyko specyficzne jest najmniejsze z możliwych. Należy zastanowić się, jak ocenić zastosowanie konkretnego indeksu w modelu indeksowym. Pełne rozważania dotyczące kryterium oceny jakości dopasowania doprowadziły do wniosku, że nie można w prosty sposób porównywać ryzyka specyficznego różnych walorów. Inaczej należy bowiem traktować ryzyko specyficzne np. o wartości 3% dla akcji, której całkowite ryzyko wynosi 4%, a inaczej dla akcji o ryzyku 10%. W celu dobrego porównania powinno się więc unormować ryzyko specyficzne poprzez podzielenie go przez ryzyko całkowite akcji. W ostateczności więc obiektywny wskaźnik średniego niedopasowania wszystkich akcji do ich modelu wyznaczany jest ze wzoru:

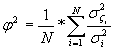(11)

Współczynnik ten jest zbliżony swoją konstrukcją do współczynnika zbieżności stosowanego np. w ekonometrii. Jego wartość zawiera się w przedziale <0 ; 1>. 0 oznacza idealne dopasowanie (ryzyko specyficzne wszystkich akcji równe zero). W miarę wzrostu wartości wskaźnika niedopasowania jakość modeli maleje. Warto tu zaznaczyć, że mniejsza wartość tego współczynnika informuje również o większej ilości informacji o całym rynku niesionej przez ten indeks. Wyliczenie średniej wartości niedopasowania dla różnych indeksów używanych w Polsce (dla wielu horyzontów czasowych) pozwala wysnuć wniosek, że oficjalnie publikowane indeksy giełdowe WIG, WIG20 i WIRR są mniej przydatne do zastosowania w analizie portfelowej niż indeksy Domów Maklerskich PENETRATOR i MAGNUS (które mogą być używane równoważnie). Jeszcze lepszym do tego celu indeksem jest COR, zaproponowany przeze mnie i Krzysztofa Mnicha. Problem ze stosowaniem tego indeksu wynika z tego, że indeks ten nie ma wartości liczonej w punktach (jak np. WIG), nie można więc narysować jego przebiegu czy opublikować go w prasie. Czytelników, których nie przerażają takie stwierdzenia jak ortogonalizacja, diagonalizacja i odwracanie macierzy odsyłam do Majowego, Czerwcowego i Lipcowego (z roku 1996) numeru miesięcznika PENETRATOR WG, w którym opisany jest sposób wyznaczania tego indeksu i zalety oraz problemy związane z jego używaniem.

Mam nadzieję, że dzisiejszy artykuł pokazał czytelnikom zaletę korzystania z uproszczenia indeksowego. W kolejnym artykule zaprezentuję modele wieloindeksowe, które są nieznacznie bardziej skomplikowane (ale i tak prostsze od modelu Markowitza), za to z punktu widzenia zarówno matematyki jak i intuicji lepiej odzwierciedlają faktyczne zachowanie akcji.

Dopisek z kwietnia 2009

Klasyczna macierz korelacji wyliczana z notowań historycznych jest zaszumionym obrazem rzeczywistej macierzy korealacji. Jednym z prostych sposobów odszumienia jest wyznaczenie wartości własnych macierzy, odrzucenie nieznaczącyh i ponowna rekonstrukacja tej macierzy z tych wartości własnych. Takie podejście to nic innego jak przejście na model jednoindeksowy (pozostawienie tylko jednej wartości własnej) lub wieloindeksowy (pozostawienie kilku wartości własnych). W ramach doświadczeń możnaby próbować wykładniczego zaniku wpływy wartości własnych na wartość macierzy korelacji. Temat do przemyśleń.